2019年第35届CMO第2题的一种纯几做法

By Carzival

题目概述

题目概述

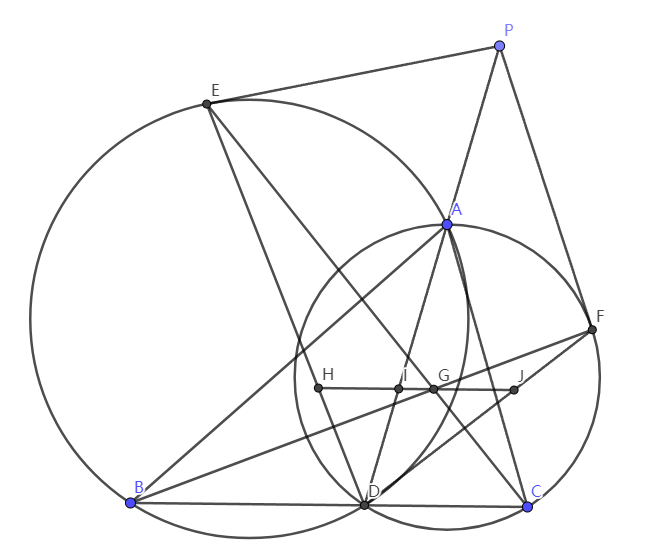
已知三角形\(\triangle{ABC}\), 角平分线\(AD\). 直线\(AD\)上一点\(P\)分别切\(\triangle{ABD}\)的外接圆于点\(E\), \(\triangle{ACD}\)的外接圆于点\(F\). \(\triangle{ABE}\),\(EC,BF\)于点\(G\). 过点\(G\)且平行于\(BC\)的直线分别交\(ED,AD,FD\)于点\(H,I,J\). 求证: \(HI=GJ\).

做题思路

今天我们物理开始讲磁力了，物理老师说钢、铁、镍一类的东西都能被磁化，我听完就悟了，大彻大悟。

课后我问老师：“老师，是不是钢和镍都可以被磁化？”

老师笑了笑，说：“是的。怎么了？”

我赶忙追问：“那我对南极点的爱是不是也可以被磁化？

老师疑惑了，问为什么？

我笑着，红了眼眶：“因为我对南极点的爱就像钢铁打造的拖拉机一样，轰轰烈烈哐哐锵锵。”

最终证明

证明：

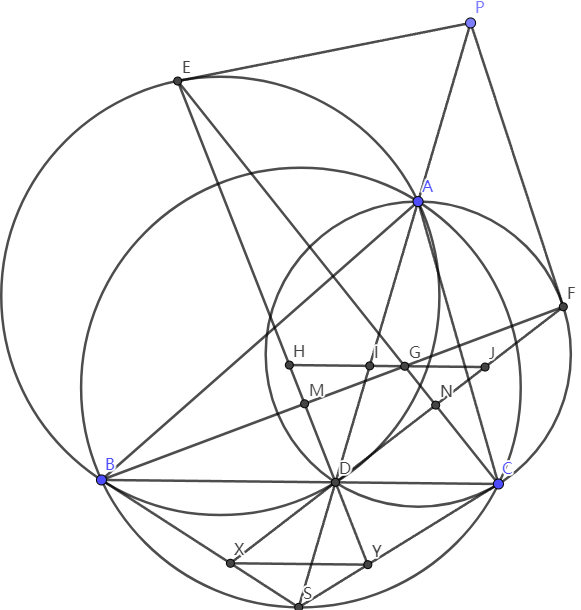
作 \(\triangle{ABC}\) 的外接圆交直线 \(AD\) 于点 \(S\).

记 \(FD\cap BS=X,ED\cap CS=Y.\)

容易知道 \(HI=GJ\Leftrightarrow\frac{HG}{GJ}=\frac{JI}{IH}\)

一方面,由 \(XY \parallel BC \parallel HJ,\) 知 \(\frac{JI}{IH} = \frac{BD}{DC}.\)

另一方面，由 \(\angle{BCS}=\angle{BAS}=\angle{BEY}\) 得 \(A,E,S,Y\) 四点共圆, 有\(AD\times DS=YD\times DE=AD\times DB,\) 同理 \(AD\times DS=XD\times DF=AD\times DB,\) 即 \(XD\times DF=YD\times DE,\) 有 \(E,F,Y,X\) 四点共圆. 又注意到 \(\angle{YEC}=\angle{YBC}=\angle{XCB}=\angle{XEB},\) 得 \(E,F,J,H\) 四点共圆, 有 \(MN \parallel XY \parallel HJ,\) 进一步有 \(\frac{HG}{GJ}=\frac{BD}{DC}.\)

这样也就证明了 \(\frac{HG}{GJ}=\frac{JI}{IH}.\)

\(\square.\)

个人见解

此题更常见的做法是证明 \(E,F,C,B\) 四点共圆，再运用正弦定理进行计算，有兴趣的读者不妨自行研究，会发现这是非常简单的。

我在刚开始做这道题时便未曾考虑计算手段，试图用蒙日定理证明 \(E,F,C,B\) 四点共圆也毫无进展，故采用了此种雕虫小技。在和询问同学、教练和查阅各解答后，我并未发现与此解答一样的纯几做法，故写出来放在这里。