一道奇怪的题¶
By Carzival
题目概述¶
题目概述
\(Rt\triangle{ABC}, AB\perp BC,\) 点\(E\)是\(AC\)中点. \(DA\perp AC\) 于 \(A,\) \(DE\cap BC=F.\) 求证: \(\angle{ABD}=\angle{CAF}\)
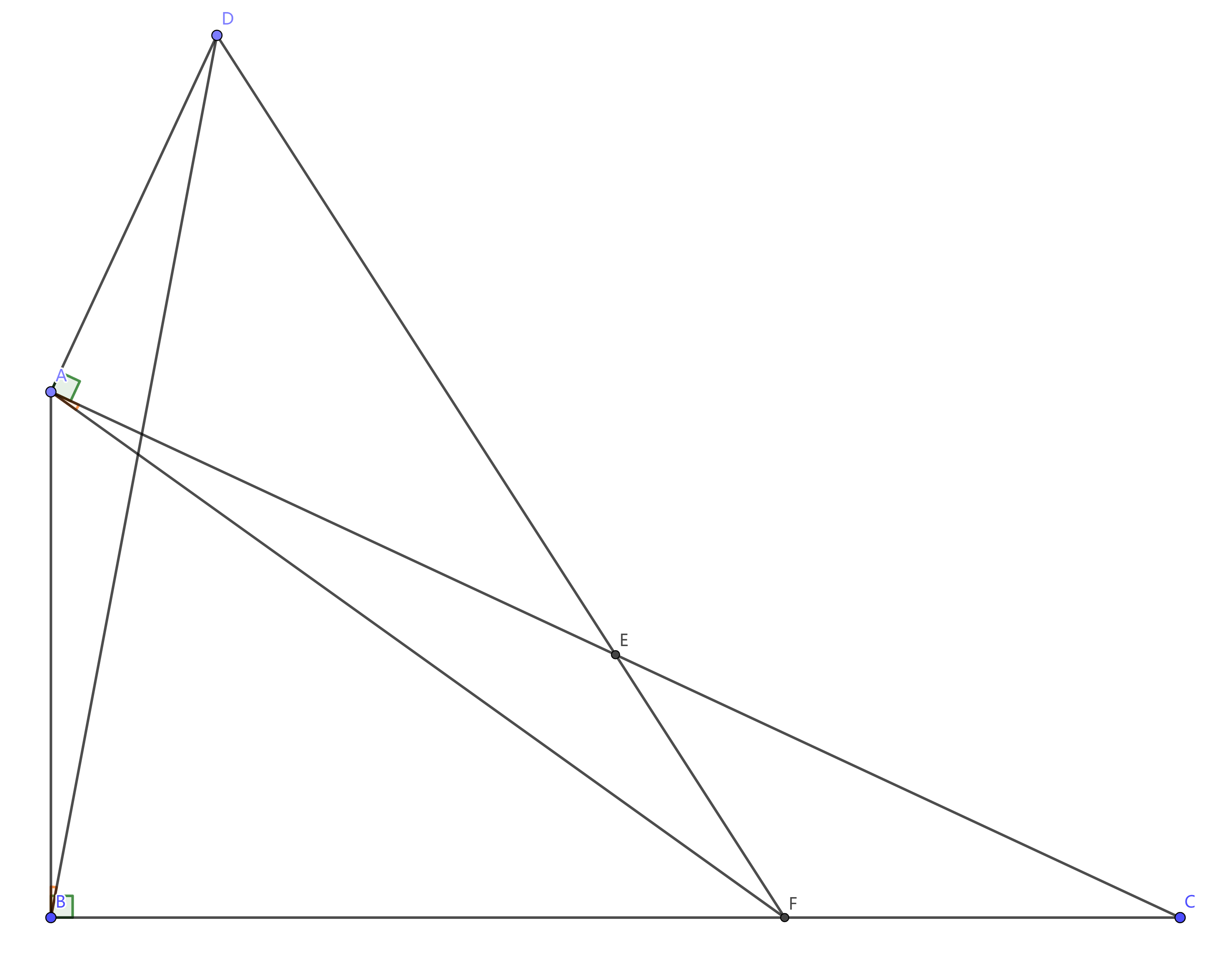
做题思路¶
看到这题我直接蚌埠住了:莫名其妙的线段和角度,丑陋的图形,见鬼的条件……但是仔细回想,我们有处理这些元素的工具吗?有的!那就是——
调和/等角关系
实际上想起它们是因为调和/等角的条件长得和本题一样奇怪
联系调和中常见的直角,我们几乎可以断定调和就是解决此题的钥匙,接下来只需要找特殊点猜关系就好了()
最终证明¶
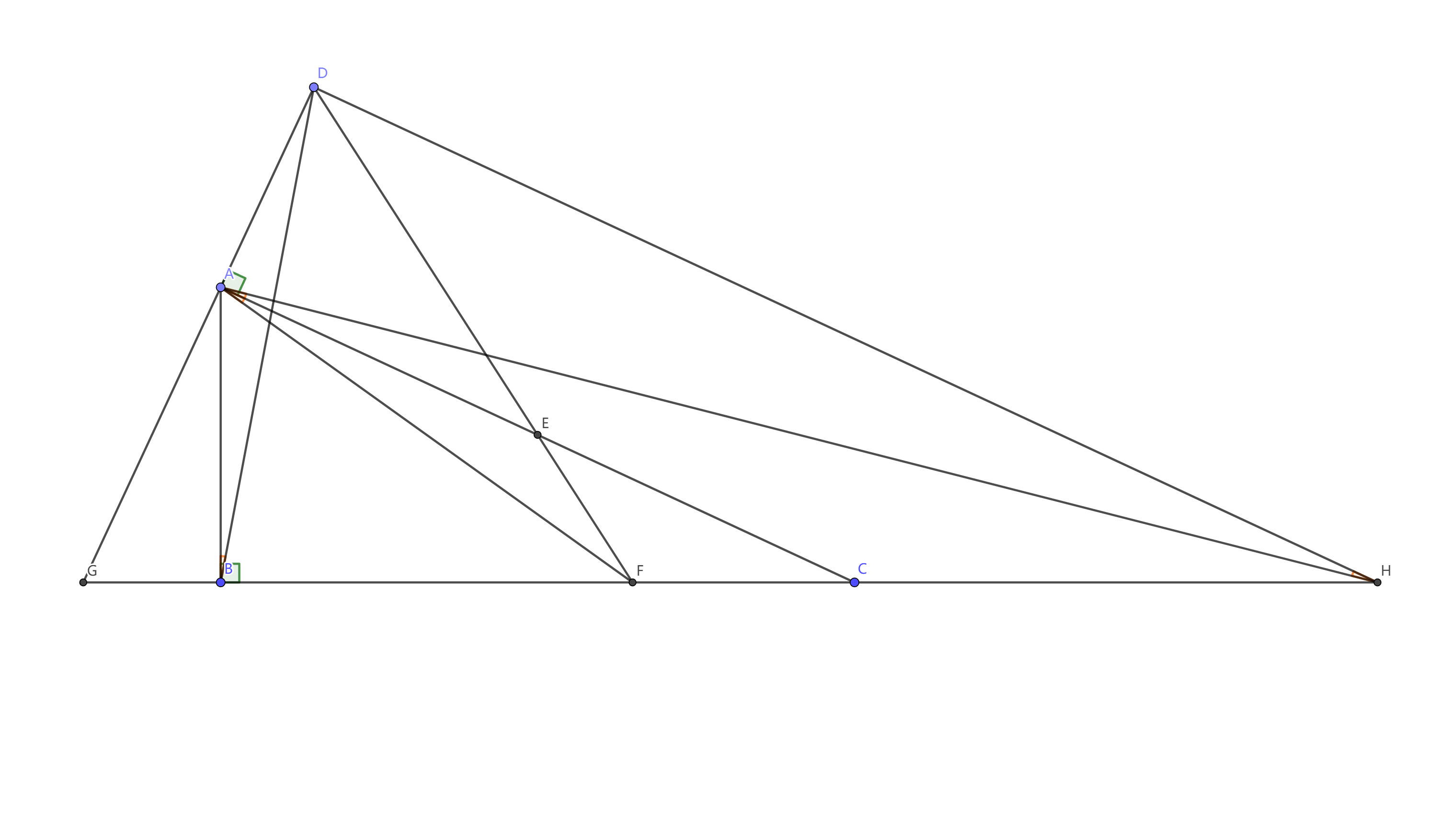
证明: 记 \(DA\cap CB=G,AC\parallel DH\cap BC=H.\)
注意到 \(DA,DC;DE,DH\) 为调和点列, 即 \(DG,DC;DF,DH\) 为调和点列, \(G,C;F,H\) 为调和点列。
又 \(\angle{GAC}=\frac{1}{2}\pi,\) 故 \(\angle{CAF}=\angle{CAH}=\angle{AHD}\)(此处由熟知结论得).
由 \(B,H,D,A\) 四点共圆, 即得 \(\angle{ABD}=\angle{AHD}=\angle{CAF}.\)
\(\square.\)
个人见解¶
这道题当然可以用构建相似之类的初中平几方法解决。但值得注意的是,此题中调和关系将支离破碎的元素和谐统一,展现了一种特殊的美感,这恐怕是使用老方法生搬硬套的人所感受不到的。